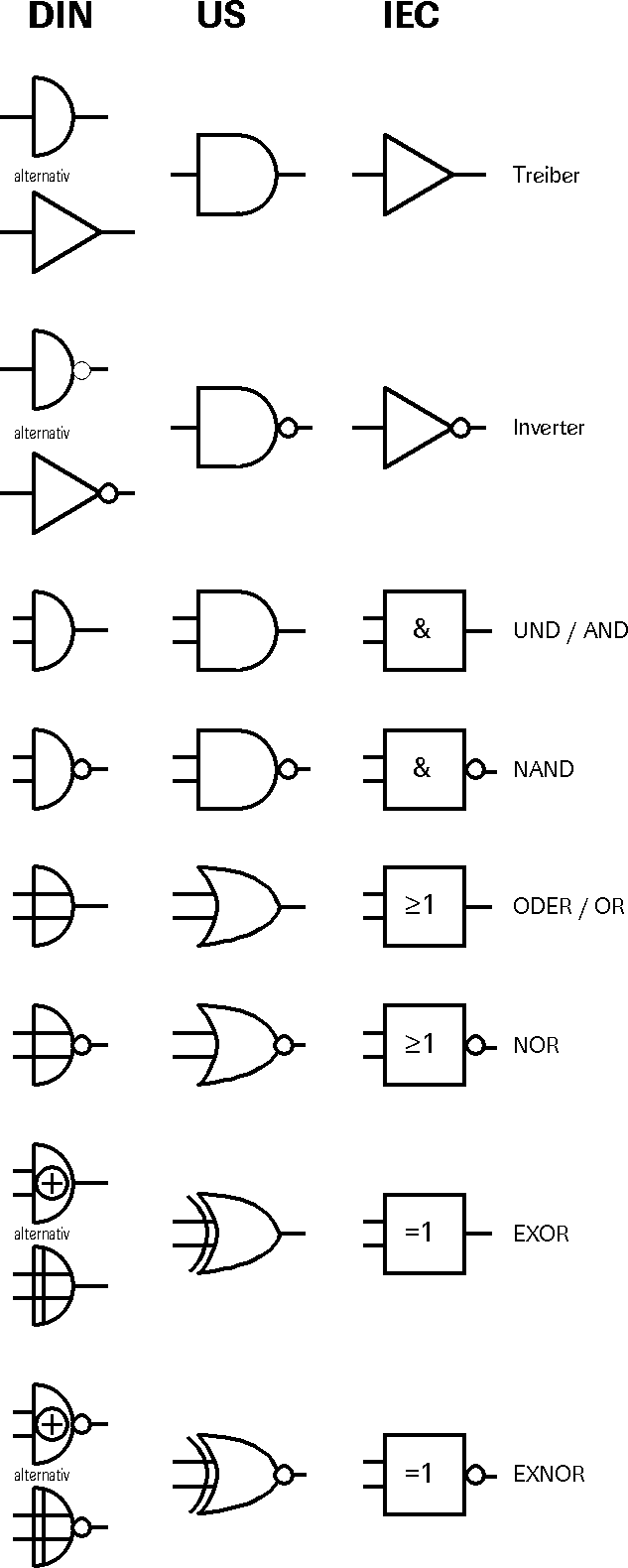
Leider hat es bei den Blocksymbolen mit der internationalen Normung wieder mal nicht geklappt, sodass Sie in Schaltplänen aus Übersee (und die meisten Typenblätter werden einfach von den hiesigen Vertreibern im Original übernommen) auf unterschiedliche Symbole treffen. Verschärft wird das Problem noch durch eine neue, angeblich internationale Norm mit der Bezeichnung IEC, die sich aber gegenüber der alten DIN-Fassung nie so richtig durchsetzen konnte. Die Gründe dafür liegen auf der Hand: Während die alten Symbole wirklich durch ihr Symbol, also ihre grafische Darstellung, zu unterscheiden sind, muss man zum Begreifen der einheitlich rechteckigen IEC-Symbole erst mal den Inhalt lesen und daraus die Funktion ableiten. Sicher, die Bedeutung der IEC-Symbole erschließt sich auch Nichtfachleuten durch Interpretation der mathematischen Symbole in den Kästchen, während die alten Symbole erst gelernt werden müssen. Doch lesen solche Symbole in der Regel Fachleute, denen auch zu lernende unterschiedliche Symbole nach kurzer Zeit eingängiger sind als optisch schwerer zu unterscheidende. Eine kurze Nachfrage bei Visualisierungsfachleuten hätte der Experten-Kommission, die die neuen Symbole verbrochen hat, sicher schnell vor Augen geführt (sic!), dass sich diese Pseudo-Symbole nie so recht durchsetzen werden. (Mir liegt ein Buch vor, in dem vorn auf 17 Seiten die Vorteile der IEC-Symbole erläutert werden, doch erstaunlicher Weise tauchen im Rest des Buches fast durchgängig US-Symbole auf!)

Bild invertieren

Allen Varianten ist gemeinsam, dass ein kleiner Kreis für eine Invertierung des Schaltzustandes sorgt. Diese Ergänzung kann sowohl am Eingang als auch am Ausgang des eigentlichen Symbols stehen.

Als hierzulande gebräuchlich kann man immer noch die alten DIN-Symbole ansehen, leichter zu erkennen sind sie auch.

Mit »Schaltern« rechnen

In den Siebziger-Jahren des vorigen Jahrhunderts wurde die Mengenlehre als Einstieg in die Grundschulmathematik benutzt. Ein sehr untaugliches Vorhaben, das dann auch schnell wieder aufgegeben wurde. Seither haftet der Mengenlehre und der mit ihr eng verbundenen Booleschen Algebra ein Ruf der Unseriosität an, den beide nicht verdient haben.

Für das Verständnis des Zusammenwirkens von Logikschaltungen ist die Boolesche Algebra unverzichtbar. Selbst Weichenstraßen lassen sich mit Booles Hilfe in mathematische Formeln fassen!

Das Stichwort Weichenstraßen gibt schon den konkreten Hinweis: Schaltalgebra beschäftigt sich mit Netzwerken von Schaltern. In dem Augenblick, da bestimmte Bedingungen in einem Netzwerk mehrfach, aber an unterschiedlichen Stellen auftreten, hilft die Schaltalgebra, dieses Netzwerk zu vereinfachen. Ich möchte Sie hier aber gar nicht mit allen Details dieser Wissenschaft langweilen, nur die wichtigsten Regeln erläutern, die Ihnen beim Entwurf einer Logikschaltung weiterhelfen können.

In der Booleschen Algebra erhält die UND-Verknüpfung das Rechenzeichen ·. Das sieht wie ein Multiplikationszeichen aus und hat auch eine gewisse Verwandtschaft in seinen operativen Auswirkungen. Wenn wir uns mit dieser Verknüpfung eine Wahrheitstabelle anlegen, wird die Ähnlichkeit zur Multiplikation deutlich:

Wahrheitstabelle UND

Egal ob Sie die Rechenregeln der üblichen Algebra für Multiplikation anwenden oder jene der Booleschen Algebra für logische Verknüpfungen, die Ergebnisse in den Schnittpunkten sind immer gleich. Ersetzen Sie nun noch gedanklich die 0 durch »negatives Potential« und die 1 durch »positives Potential«, haben Sie auch den Schritt zur elektronischen Schaltalgebra vollzogen.

Inv

0

1

1

0

UND

0

1

Inv

NAND

0

1

0

0

0

·

0

1

=

0

1

1

1

0

1

1

0

1

1

0

ODER

0

1

0

0

1

1

1

1

ODER

0

1

Inv

NOR

0

1

0

0

1

·

0

1

=

0

1

0

1

1

1

1

0

1

0

0

Was hier rein mathematisch geklappt hat, lässt sich natürlich auch in Blocksymbolen darstellen. Diese Kombination funktioniert auch in der Gegenrichtung: Ein NAND-Gatter mit nachgeschaltetem Inverter wird wieder zum UND-Gatter, ein NOR-Gatter mit nachgeschaltetem Inverter zu ODER.
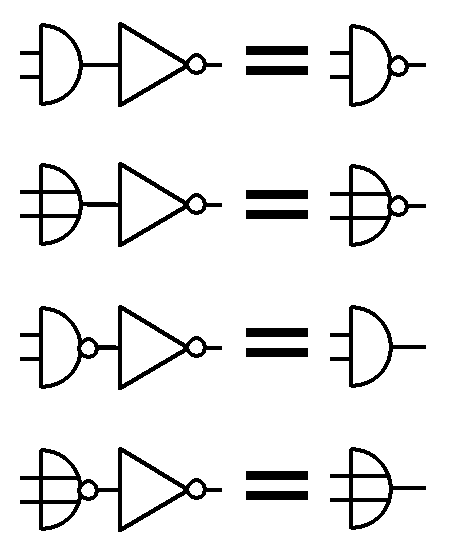